Need help? We're here to assist you!
Thank You for Enquiry, we will contact you soon!
Close
The Class 9 is an important year in a student’s life and Maharashtra State Board Maths 2 is one of the subjects that require dedication, hard work, and practice. It’s a subject where you can score well if you are well-versed with the concepts, remember the important formulas and solving methods, and have done an ample amount of practice. Worry not! Home Revise is here to make your Class 9 journey even easier. It’s essential for students to have the right study material and notes to prepare for their board examinations, and through Home Revise, you can cover all the fundamental topics in the subject and the complete Maharashtra State Board Class 9 Maths 2 Book syllabus.

Practice Set 4.1 Page 53
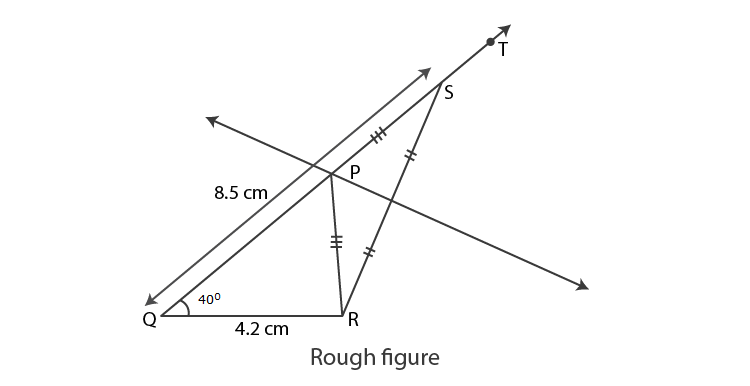
1. Construct PQR, in which QR = 4.2 cm, mQ = 40° and PQ + PR = 8.5 cm
Solution :
Let us first draw a rough figure of expected triangle.
Explanation :
As shown in the rough figure, first we draw seg QR = 4.2 cm of length.
Draw a ray QT making an angle of 40° with seg QR.
Mark point S on QT such that QS = 8.5cm
Now QP+PS = QS [Q-P-S]
QP+PS = 8.5 cm ….(i)
Given PQ+PR = 8.5 cm ……(ii)
QP+PS = PQ+PR [From (i) and (ii)]
PS = PR
P is on perpendicular bisector of SR.
The point of intersection of ray QT and perpendicular bisector of ray SR is point P.
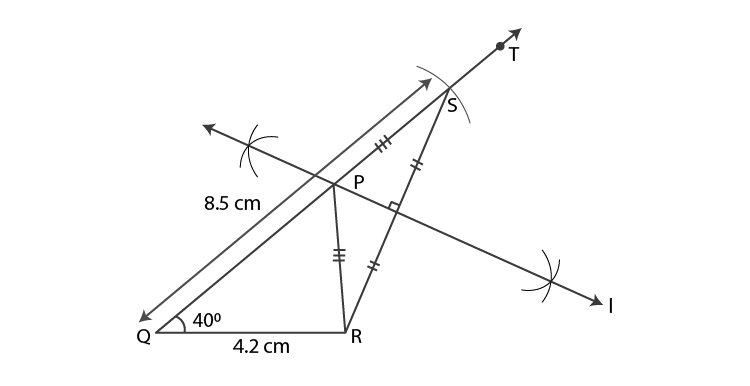
Steps of construction:
(1)Draw segment QR of length 4.2 cm.
(2)Draw ray QT such that mTQR = 40°.
(3)Mark point S on ray QT such that d(Q,S) = 8.5 cm.
(4)Draw seg SR.
(5)Draw perpendicular bisector of SR which intersect ray QT. Mark the point as P.
(6)Draw seg PR.
PQR is the required triangle.
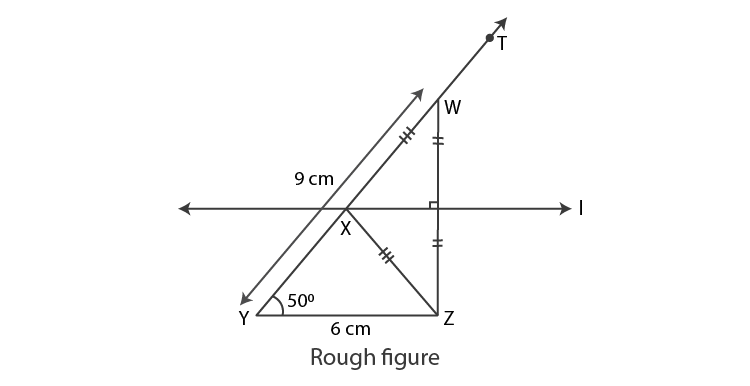
2. Construct XYZ, in which YZ = 6 cm, XY + XZ = 9 cm. XYZ = 50°
Solution:
Let us first draw a rough figure of expected triangle.
Explanation :
As shown in the rough figure, first we draw seg YZ = 6 cm of length.
Draw a ray YT making an angle of 50° with seg YZ.
Mark point W on YT such that YW = 9 cm
Now, YX+XW = YW [Y-X-W]
YX+XW = 9 cm ….(i)
Given XY + XZ = 9 cm …(ii)
YX+XW = XY + XZ [From (i) and (ii)]
XW = XZ
X is on perpendicular bisector of seg WZ.
The point of intersection of ray YT and perpendicular bisector of ray WZ is point X.
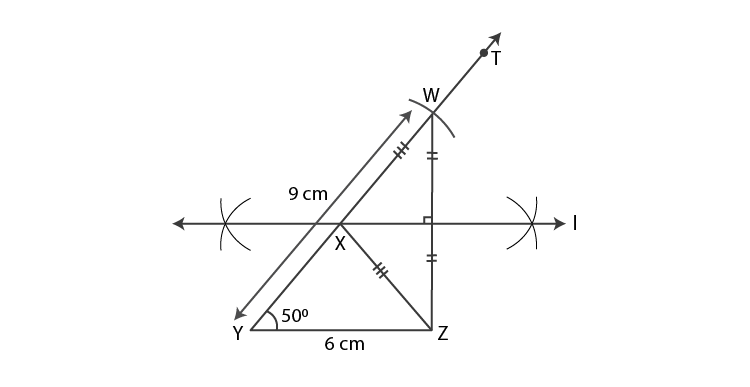
Steps of construction:
(1)Draw segment YZ of length 6 cm.
(2)Draw ray YT such that mZYT = 50°.
(3)Mark point W on ray YT such that d(Y,W) = 9 cm.
(4)Draw seg WZ.
(5)Draw perpendicular bisector of WZ which intersect ray YT. Mark the point as X.
(6)Draw seg XZ.
XYZ is the required triangle.
3. Construct ABC, in which BC = 6.2 cm, ACB = 50°, AB + AC = 9.8 cm.
Solution:
Let us first draw a rough figure of expected triangle.
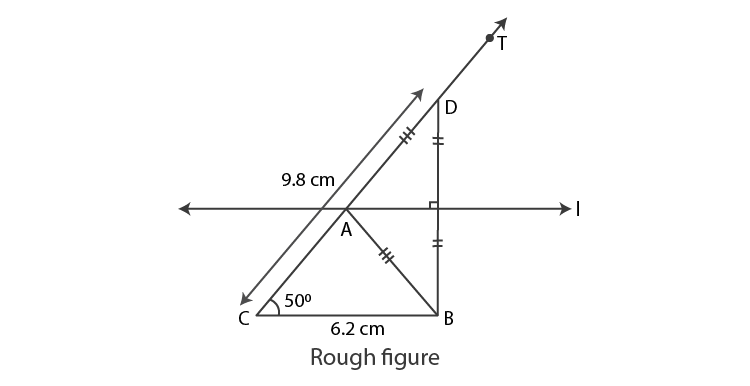
Explanation :
As shown in the rough figure, first we draw seg CB = 6.2 cm of length.
Draw a ray CT making an angle of 50° with seg CB.
Mark point D on CT such that CD = 9.8 cm
Now, CA+AD = CD [C-A-D]
CA+AD = 9.8 cm ….(i)
Given AB+AC = 9.8 cm …(ii)
CA+AD = AB+AC [From (i) and (ii)]
AD = AB
A is on perpendicular bisector of seg BD.
The point of intersection of ray CT and perpendicular bisector of ray BD is point A.
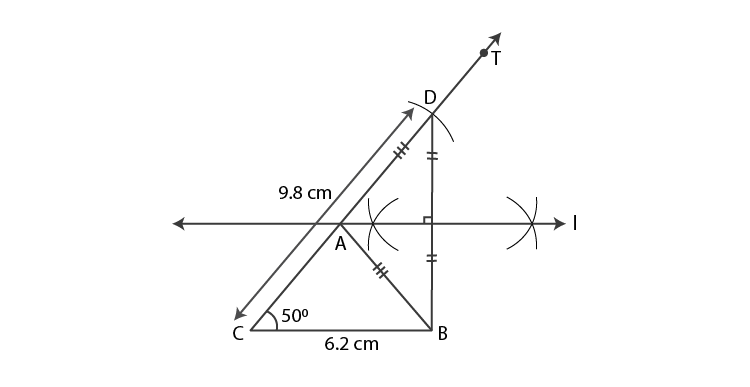
Steps of construction:
(1)Draw segment CB of length 6.2 cm.
(2)Draw ray CT such that mBCT = 50°.
(3)Mark point D on ray CT such that d(C,D) = 9.8 cm.
(4)Draw seg DB.
(5)Draw perpendicular bisector of BD which intersect ray CT. Mark the point as A.
(6)Draw seg AB.
ABC is the required triangle.
4. Construct ABC, in which BC = 5.2 cm, ACB = 45° and perimeter of ABC is 10 cm.
Solution:
Given perimeter of ABC = 10 cm
i.e, AB+BC+AC = 10 cm
AB+5.2+AC = 10 [Given BC = 5.2]
AB+AC = 10-5.2 = 4.8 cm.
The sum of two sides of a triangle is greater than the third side.
Here the sum of two sides is less than third side.
AB+AC BC
So the construction is not possible.
Practice Set 4.2 Page 54
1. Construct XYZ, such that YZ = 7.4 cm, XYZ = 45° and XY –XZ = 2.7 cm.
Solution:
Let us draw a rough figure.
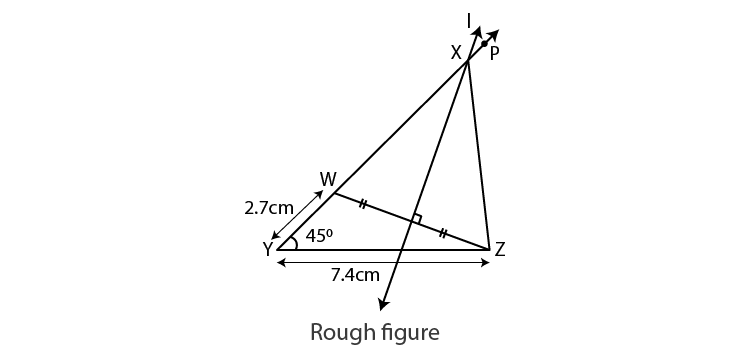
Explanation :
XY-XZ = 2.7 cm
XY >XZ.
Draw seg YZ = 7.4 cm.
We can draw the ray YP such that PYZ = 45°.
We have to locate point W on ray YP.
Take point W on ray YP such that YW = 2.7 cm.
Now , Y-W-X and
YW = XY-XW = 2.7 cm …(i)
Given XY-XZ = 2.7 cm ..(ii)
XY-XW = XY-XZ [From (i) and (ii)]
XW = XZ
Point X is on the perpendicular bisector of seg ZW.
Point X is the intersection of ray YP and the perpendicular bisector of seg ZW.
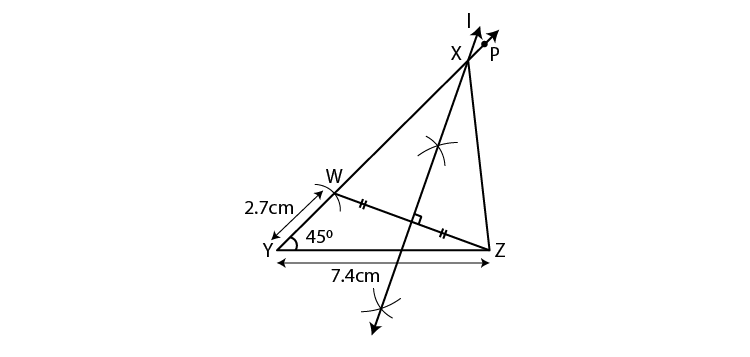
Steps of construction:
(1)Draw segment YZ of length 7.4 cm.
(2)Draw ray YP such that mPYZ = 45°.
(3)Mark point W on ray YP such that d(Y,W) = 2.7 cm.
(4)Draw seg ZW.
(5)Draw perpendicular bisector of WZ which intersect ray YP. Mark the point as X.
(6)Draw seg XZ.
XYZ is the required triangle.
2. Construct PQR, such that QR = 6.5 cm, PQR = 60° and PQ –PR = 2.5 cm.
Solution:
Let us draw a rough figure.
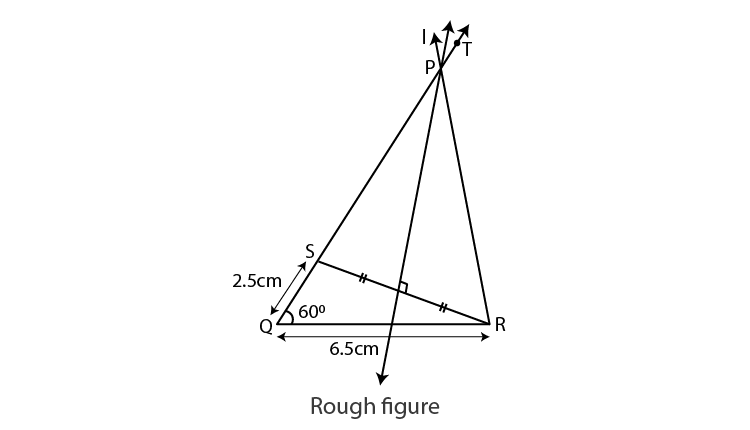
Explanation :
PQ-PR = 2.5 cm.
PQ >PR.
Draw seg QR = 6.5 cm.
We can draw the ray QT such that TQR = 60°.
We have to locate point S on ray QT.
Take point S on ray QT such that QS = 2.5 cm.
Now , Q-S-P and
QS = PQ-PS = 2.5 cm …(i)
Given PQ-PR = 2.5 cm. ..(ii)
PQ-PS = PQ-PR [From (i) and (ii)]
PS = PR
Point P is on the perpendicular bisector of seg RS.
Point P is the intersection of ray QT and the perpendicular bisector of seg RS.
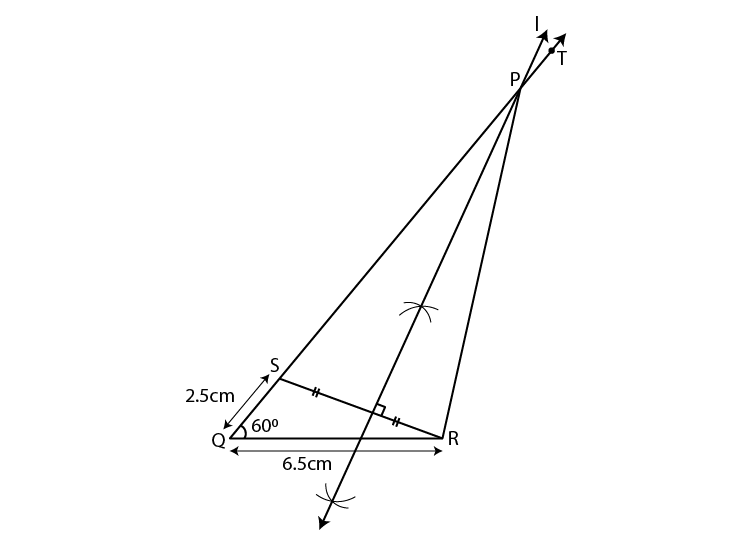
Steps of construction:
(1)Draw segment QR of length 6.5 cm.
(2)Draw ray QT such that mTQR = 60°.
(3)Mark point S on ray QT such that d(Q,S) = 2.5 cm.
(4)Draw seg SR.
(5)Draw perpendicular bisector of SR which intersect ray QT. Mark the point as P.
(6)Draw seg PR.
PQR is the required triangle.
3. Construct ABC, such that BC = 6 cm, ABC = 100° and AC –AB = 2.5 cm.
Solution:
Let us draw a rough figure.
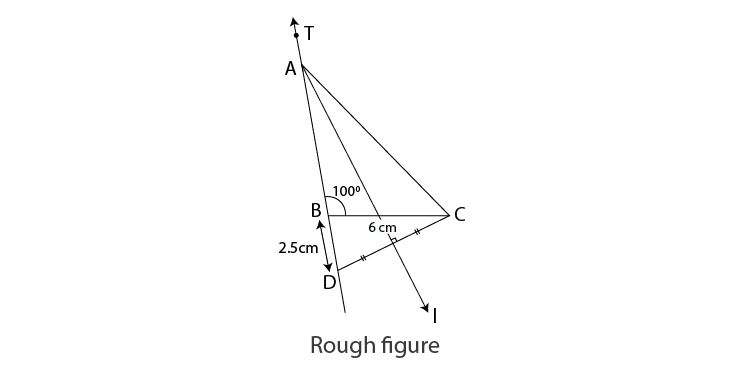
Explanation :
AC-AB = 2.5 cm.
AC >AB.
Draw seg BC = 6 cm.
We can draw the ray BT such that TBC = 100°.
We have to locate point D on opposite ray BT.
Take point D on opposite ray BT such that BD = 2.5 cm.
Now , A-B-D and
BD = AD-AB = 2.5 cm …(i)
Given AC-AB = 2.5 cm. ..(ii)
AD-AB = AC-AB [From (i) and (ii)]
AD = AC
Point A is on the perpendicular bisector of seg DC.
Point A is the intersection of ray BT and the perpendicular bisector of seg DC.
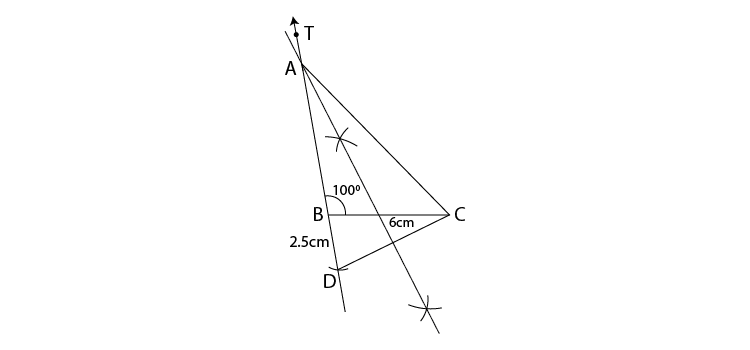
Steps of construction:
(1)Draw segment BC of length 6 cm.
(2)Draw ray BT such that mTBC = 100°.
(3)Mark point D on opposite ray BT such that d(B,D) = 2.5 cm.
(4)Draw seg DC.
(5)Draw perpendicular bisector of DC which intersect ray BT. Mark the point as A.
(6)Draw seg AC.
ABC is the required triangle.
Practice Set 4.3 Page 56
1. Construct PQR, in which Q = 70°, R = 80° and PQ + QR + PR = 9.5 cm.
Solution :
Let us draw a rough figure.
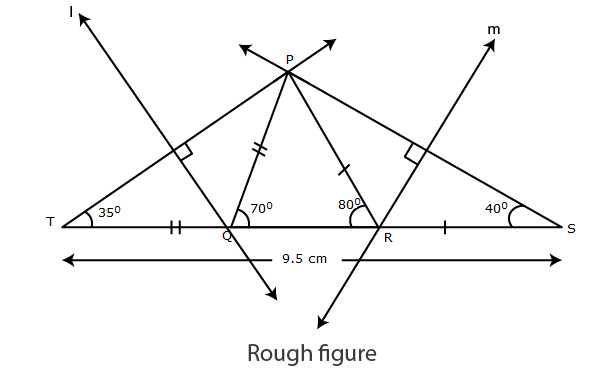
Explanation :
As shown in the figure, points T and S are taken on line QR such that,
QT = PQ, and PR = RS …(i)
TS = TQ+QR+RS
TS = PQ+QR+PR ….(ii) [from (i)]
Given PQ + QR + PR = 9.5 cm. …(iii)
TS = 9.5cm [from (ii) and (iii)]
Now in PTQ, TQ = QP [from (i)]
QPT = QTP = x˚ …(iv) [Isoceles triangle theorem]
In PQT, PQR is the exterior angle.
QPT+QTP = PQR [Remote interior angle theorem]
x+x = 70˚ [From (iv)]
2x = 70˚
x = 70/2 = 35˚
PTQ = 35 ˚
T = 35˚
Similarly, S = 40˚.
Now in PTS
T = 35°, S = 40° and TS = 9.5 cm
Hence, we can draw PTS .
Since, PQ = TQ,
Point Q lies on perpendicular bisector of seg PT.
Also, RP = RS
Point R lies on perpendicular bisector of seg PS.
Points Q and R can be located by drawing the perpendicular bisector of PT and PS respectively.
PQR can be drawn.
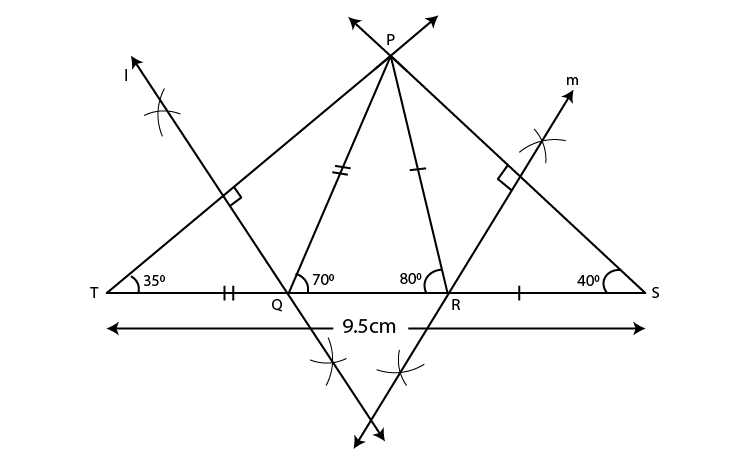
Steps of construction:
1. Draw seg TS of length 9.5 cm.
2. From point T draw ray making angle of 35°.
3. From point S draw ray making angle of 40°.
4. Mark the point of intersection of two rays as P.
5. Draw the perpendicular bisector of seg PT and seg PS intersecting seg TS in Q and R respectively.
6. Join PQ and PR.
Hence, PQR is the required triangle.
2. Construct XYZ, in which Y = 58°, X = 46° and perimeter of triangle is 10.5 cm.
Solution:
Let us draw a rough figure.
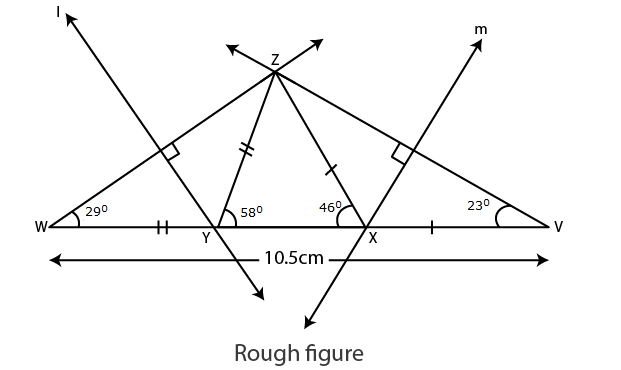
Explanation :
As shown in the figure, points W and V are taken on line YX such that,
YW = ZY and XV = ZX ……(i)
YW+YX+XV = WV [W-Y-X, Y-X-V]
ZY+YX+XZ = WV ……(ii) [From (i)]
Also,
ZY+YX +XZ = 10.5 cm …..(iii) [Given perimeter is 10.5 cm]
WV = 10.5 cm [From (ii) and (iii)]
In ZWY
YZ = YW [From (i)]
YZW = YWZ = x° …..(iv) [Isosceles triangle theorem]
In ZYW, ZYX is the exterior angle.
YZW +YWZ = ZYX [Remote interior angles theorem]
x+x = 58° [From (iv)]
2x = 58°
x = 58/2 = 29°
ZWY = 29°
YZW = 29°
Similarly, V = 23°
Now, in ZWV
W = 29°, V = 23° and
WV= 10.5 cm
Hence, we can draw ZWV .
Since, ZY = YW
Point Y lies on perpendicular bisector of seg ZW.
Also, ZX = XV
Point X lies on perpendicular bisector of seg ZV.
Points Y and X can be located by drawing the perpendicular bisector of ZW and ZV respectively.
XYZ can be drawn.
Steps of construction:
1. Draw seg WV of length 10.5 cm.
2. From point W draw ray making angle of 29°.
3. From point V draw ray making angle of 23°.
4. Mark the point of intersection of two rays as Z.
5. Draw the perpendicular bisector of seg WZ and seg VZ intersecting seg WV in Y and X respectively.
6. Join XY and XX.
Hence, XYX is the required triangle.
Problem Set 4 Page 56
1. Construct XYZ, such that XY + XZ = 10.3 cm, YZ = 4.9 cm, XYZ = 45°.
Solution:
Let us draw a rough figure.
As shown in the rough figure draw segYZ = 4.9cm
Draw a ray YT that makes an angle of 45° with YZ.
Mark a point W on ray YT,
so that YW= 10.3 cm
Now,YX + XW = YW [Y-X-W]
YX + XW=10.3cm …..(i)
Given, XY + XZ = 10.3cm ……(ii)
YX + XW = XY + XZ [From (i) and (ii)]
XW = XZ
Point X is on the perpendicular bisector of seg WZ
The point of intersection of ray YT and perpendicular bisector of seg WZ is point X.
Steps of construction:
1. Draw seg YZ of length 4.9 cm.
2. Draw ray YT, so that ZYT = 45°.
3. Mark point W on ray YT such that l (YW) = 10.3 cm.
4. Draw seg WZ.
5. Draw perpendicular bisector of seg WZ intersecting ray YT. Mark the point as X.
6. Draw seg XZ.
XYZ is the required triangle.
2. Construct ABC, in which B = 70°, C = 60°, AB + BC + AC = 11.2 cm
Solution:
Let us draw a rough figure.
As shown in the figure, take point D and E on line BC, so that
BD = AB and CE = AC ……(i)
BD+BC+CE = DE [D-B-C, B-C-E]
AB+BC+AC = DE …..(ii)
Given AB+BC+AC= 11.2 cm ….(iii)
DE = 11.2 cm [From (ii) and (iii)]
In ADB
AB = BD [From (i)]
BAD = BDA = x° ….(iv) [Isosceles triangle theorem]
In ABD, ABC is the exterior angle.
BAD +BDA = ABC [Remote interior angle theorem]
x+x = 70° [From (iv)]
2x = 70°
x = 70/2 = 35°
ADB = 35°
D = 35°
Similarly, E = 30°
Now, in ADE
D = 35°, E = 30° and DE = 11.2 cm
So, ADE can be drawn.
Since, AB = BD
Point B lies on perpendicular bisector of seg AD.
Also AC = CE
Point C lies on perpendicular bisector of seg AE.
Points B and C can be located by drawing the perpendicular bisector of AD and AE respectively.
So, ABC can be drawn.
Steps of construction:
1. Draw seg DE of length 11.2 cm.
2. From point D draw ray making angle of 35°.
3. From point E draw ray making angle of 30°.
4.Mark the point of intersection of two rays as A.
5. Draw the perpendicular bisector of seg DA and seg EA intersecting seg DE in B and C respectively.
6. Draw seg AB and seg AC.
ABC is the required triangle.
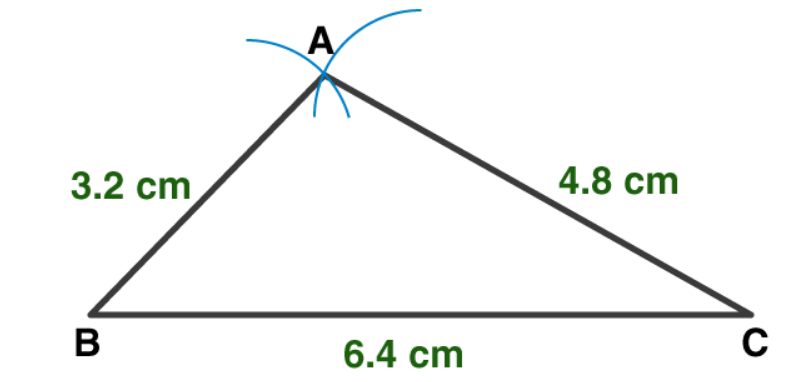
3. The perimeter of a triangle is 14.4 cm and the ratio of lengths of its side is 2 : 3 : 4. Construct the triangle.
Solution:
Let us draw a rough figure.
Let the common multiple be k
In ABC,
AB = 2k cm, AC = 3k cm, BC = 4k cm
Given the perimeter of triangle = 14.4 cm
AB+BC+AC = 14.4
2k+3k+4k = 9k
9k = 14.4
k = 14.4/9
k = 1.6
AB = 2k = 2×1.6 = 3.2 cm
AC = 3k = 3×1.6 = 4.8 cm
BC = 4k = 4×1.6 = 6.4 cm
Steps of construction:
1.Draw seg BD = 6.4 cm.
2.With B as centre, draw an arc of radius 3.2 cm.
3.With C as centre, draw an arc of radius 4.8 cm so that it intersects the previous arc at point A.
4.Join AB and AC.
So ABC is the required triangle.
4. Construct PQR, in which PQ –PR = 2.4 cm, QR = 6.4 cm and PQR = 55°.
Solution:
Let us draw a rough figure.
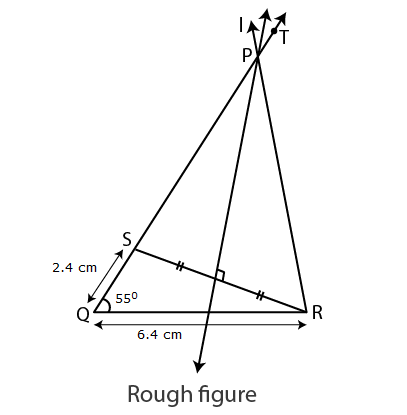
Explanation :
PQ-PR = 2.4 cm.
PQ >PR.
Draw seg QR = 6.4 cm.
We can draw the ray QT such that TQR = 55°.
We have to locate point S on ray QT.
Take point S on ray QT such that QS = 2.4 cm.
Now , Q-S-P and
QS = PQ-PS = 2.4 cm …(i)
Given PQ-PR = 2.4 cm. ..(ii)
PQ-PS = PQ-PR [From (i) and (ii)]
PS = PR
Point P is on the perpendicular bisector of seg RS.
Point P is the intersection of ray QT and the perpendicular bisector of seg RS.
Steps of construction:
(1)Draw segment QR of length 6.4 cm.
(2)Draw ray QT such that mTQR = 55°.
(3)Mark point S on ray QT such that d(Q,S) = 2.4 cm.
(4)Draw seg SR.
(5)Draw perpendicular bisector of SR which intersect ray QT. Mark the point as P.
(6)Draw seg PR.
PQR is the required triangle.
